A Cooper Tire engineer explains the use of multiscale structural analysis in modeling tire composite structures.
The composite nature of many of the components that comprise the typical tire structure requires sophisticated modeling capabilities. Micromechanics has been used to efficiently analyze tire performance on the macroscale by minimizing the loss of information afforded by elements at much smaller scales. This article discusses two examples of leveraging multiscale structural analysis technologies to analyze tire performance at multiple scales. The first example is the micromechanics analysis of the bead structure, which facilitates efficient high-fidelity bead unseating simulations. The second example is a cross-sectional analysis of tire tread-band structural design.
Bead structure analysis
Beads for pneumatic tires usually comprise many turns of hard drawn steel wire. The multiple wire feature ensures a degree of lateral flexibility while maintaining the hoop stiffness. This composite configuration enables the key anisotropic structural function, fitting and anchoring the inflated tire to the rim to maintain driving and braking reactions.1,2 Several bead unseating tests have been standardized to ensure the tire has adequate resistant capabilities against high lateral forces such as during severe turning maneuvers,
curb scrubbing or negotiating deep ruts in the roadway. During a bead unseating test, an anvil pushes the bead bundle over the interior safety hump of the rim, and the inflation pressure within the tire cavity is released.
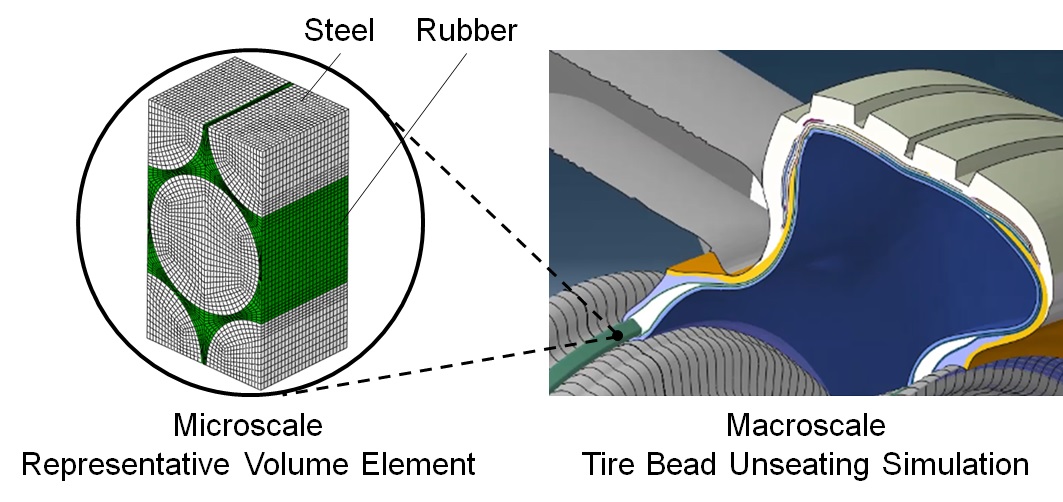
Due to the large non-linearity of the bead unseating physics, a high-performance computer is used to virtually capture the details of contact, deformation and friction. However, it is computationally expensive to include the detailed mesh of bead wire and rubber coating with elements of about 0.05mm into the unseating simulation, especially when the model is processed by an explicit solver. Therefore, the multiscale structural analysis approach is used to tackle this type of numerical prediction, as shown in Figure 1. First, the representative volume element (RVE) analysis is conducted to homogenize the anisotropic material properties of the bead bundle. Then, the effective material properties are assigned to the bead bundle in the tire bead unseating simulation, in which a much larger element size is used to mesh the model. The homogenized bead element size is about 1.5mm in the bead unseating simulation. After homogenization, the bead component is modeled as an orthotropic material. The local fields in the wire and rubber coating are not captured in the tire level simulation but can be recovered by the RVE using the bead deformation resulting from the tire level simulation.
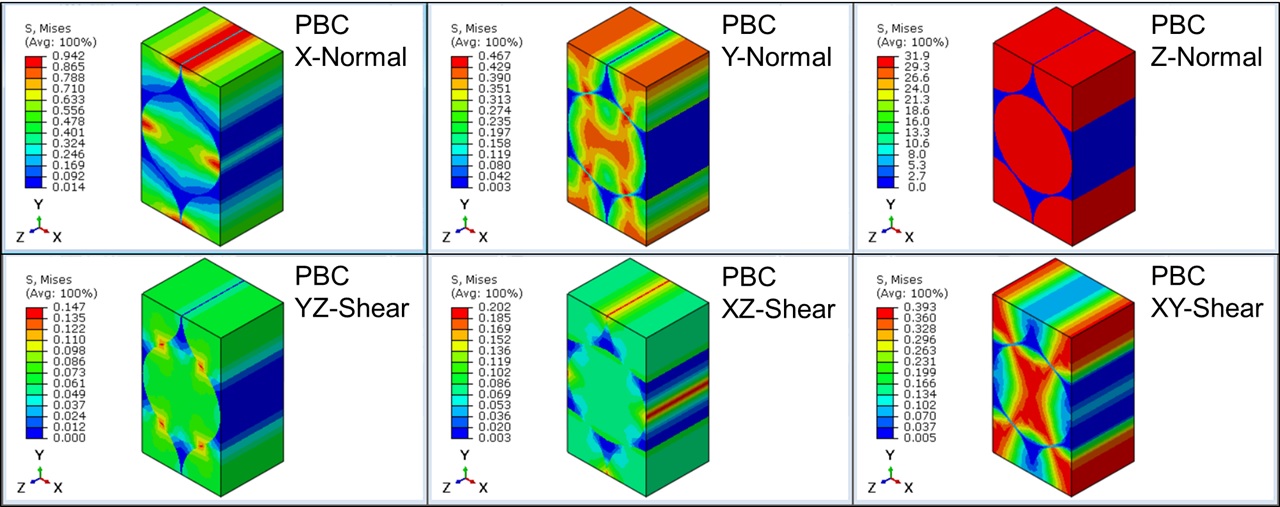
During the RVE analysis, periodic boundary condition (PBC),3 is applied to the representative volume element, which contains one unit cell of the hexagonal array shown in Figure 2. The advantage of the PBC is that the results will consistently remain the same regardless of whether the RVE contains one or multiple unit cells. This avoids additional convergence procedures when other boundary conditions are applied. Figure 2 lists the Von Mises stress fields in the RVE results from applying the periodic boundary conditions. It can be seen that the deformed RVE is still able to duplicate itself as it behaves as a material point in the bead bundle.
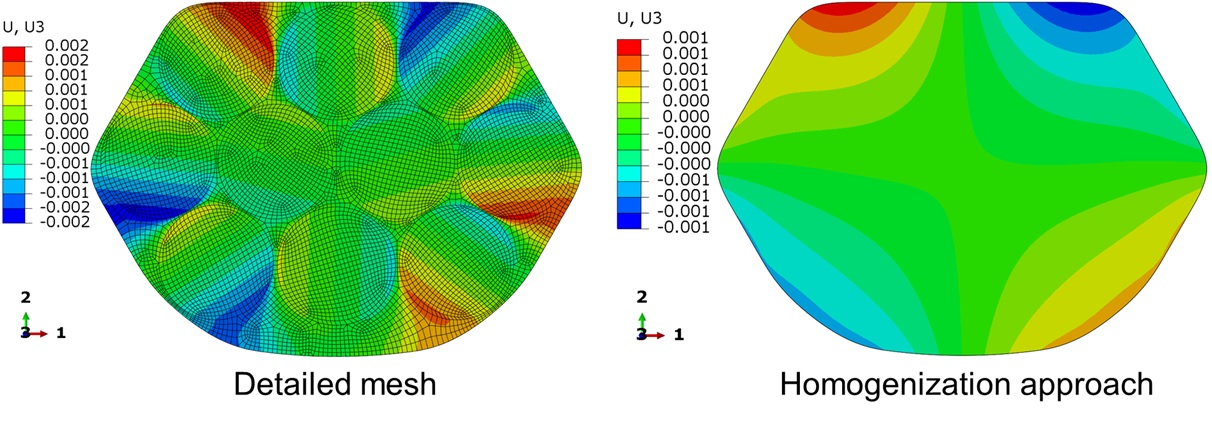
Obtaining RVE results, we can use the effective homogenized bead material property in tire level simulations. It is also worth mentioning that the bead is subjected to longitudinal twisting (Figure 1) because of the anvil acting on the sidewall. Therefore, the longitudinal warping field that results from the twisting also affects the effective homogenized bead material properties. The longitudinal warping field is defined by the out-of-plane displacements of the material points on the cross-section of the bead. Figure 3 compares the longitudinal warping displacements on the bead cross-sections obtained from using detailed mesh and a homogenization approach.
Tread-band structural design
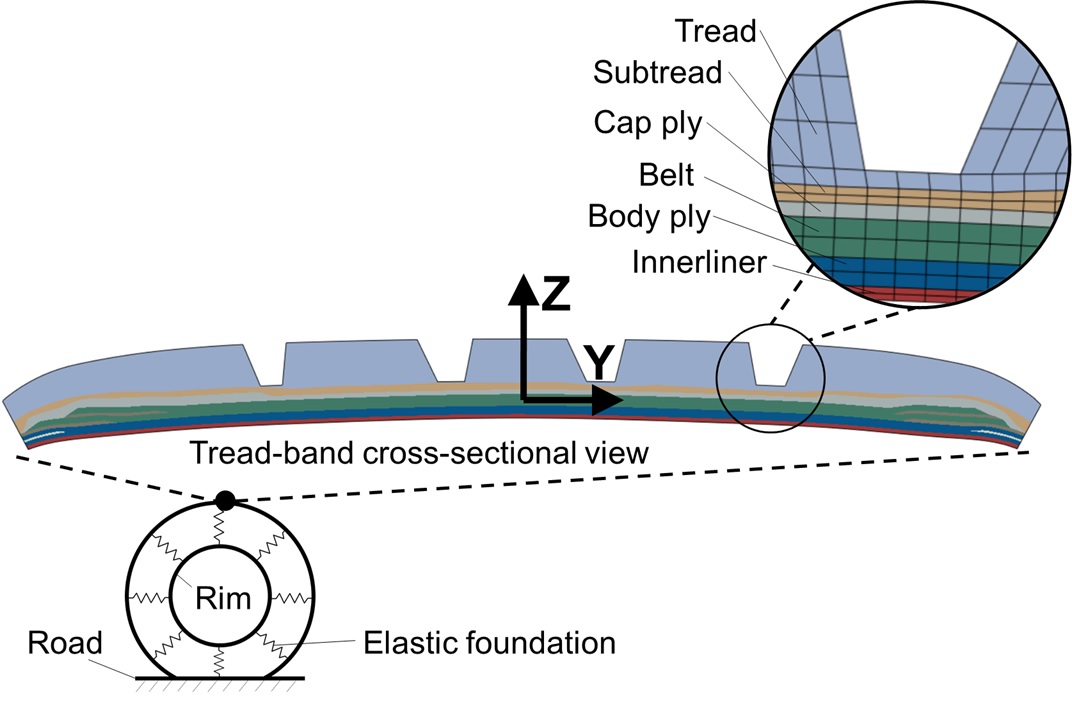
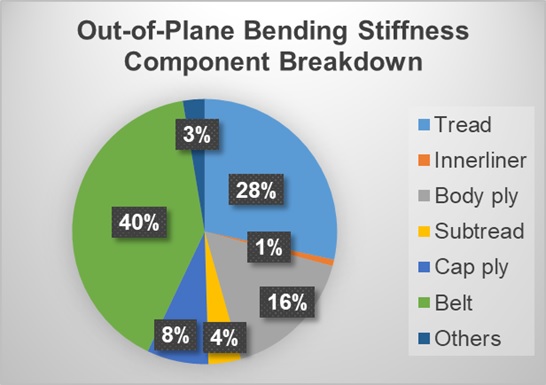
Several tire performance characteristics (such as cornering properties, vibration and the contact patch) are closely related to the bending stiffness of the composite structure of the tread band, which typically consists of tread, subtread, cap-ply, belt, body ply and innerliner (Figure 4). Because three-dimensional finite element models are computationally expensive, dimensionally simplified models are favored due to the rapid explicit format of their solutions. Herein, we focus on discussing the constitutive behavior of the tread band as shown in Figure 4, by homogenizing the heterogeneous material property field of tread-band composite to obtain the out-of-plane bending stiffness.
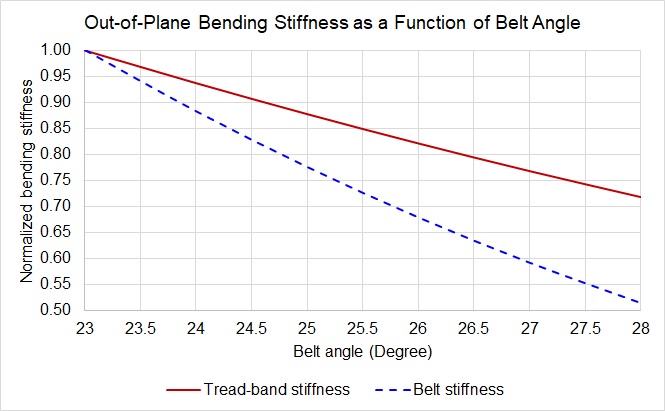
It is pointed out by Nakajima4 that the out-of-plane bending stiffness of a belt decreases by increasing belt angle and decreasing belt thickness. Bending stiffness of the composite structure has been studied using several approaches developed within the composite materials and structures community. One of these approaches is the composite beam theory. This approach is leveraged herein to estimate the out-of-plane bending stiffness of the tread band shown in Figure 4. The component breakdown of the out-of-plane bending stiffness is illustrated in Figure 5. Figure 6 shows the sensitivity of tread band and belt out-of-plane bending stiffness with respect to the belt angle as a design parameter.
Summary
In this study, multiscale structural analysis is used to model the mechanics of tire composite structures. Micromechanics analysis of bead structure and composite beam modeling of the tread-band cross-section demonstrate that the multiscale structural analysis approach not only enables efficiency in large model simulation but also facilitates the layout design for tire performance.
References
1) Clark, Samuel K, Mechanics of Pneumatic Tires, US Government Printing Office, Washington DC (1981).
2) Gent, Alan N, and Walter, Joseph D, The Pneumatic Tire, NHTSA, Washington DC (2005).
3) Yu, Wenbin, ‘Chapter 5 Micromechanics’, Multiscale Structural Mechanics, John Wiley & Sons Inc (2017), 262-266.
4) Nakajima, Yukio, ‘Chapter 11 Cornering Properties of Tires’, Advanced Tire Mechanics, Springer, Singapore, (2019), 729-730.
Fang Jiang, PhD
Engineer II, Predictive Technology
Cooper Tire & Rubber Company
701 Lima Ave., Findlay, OH 45840, USA
Email: FXJiang@coopertire.com
The author thanks Cooper Tire for support and permission for publication